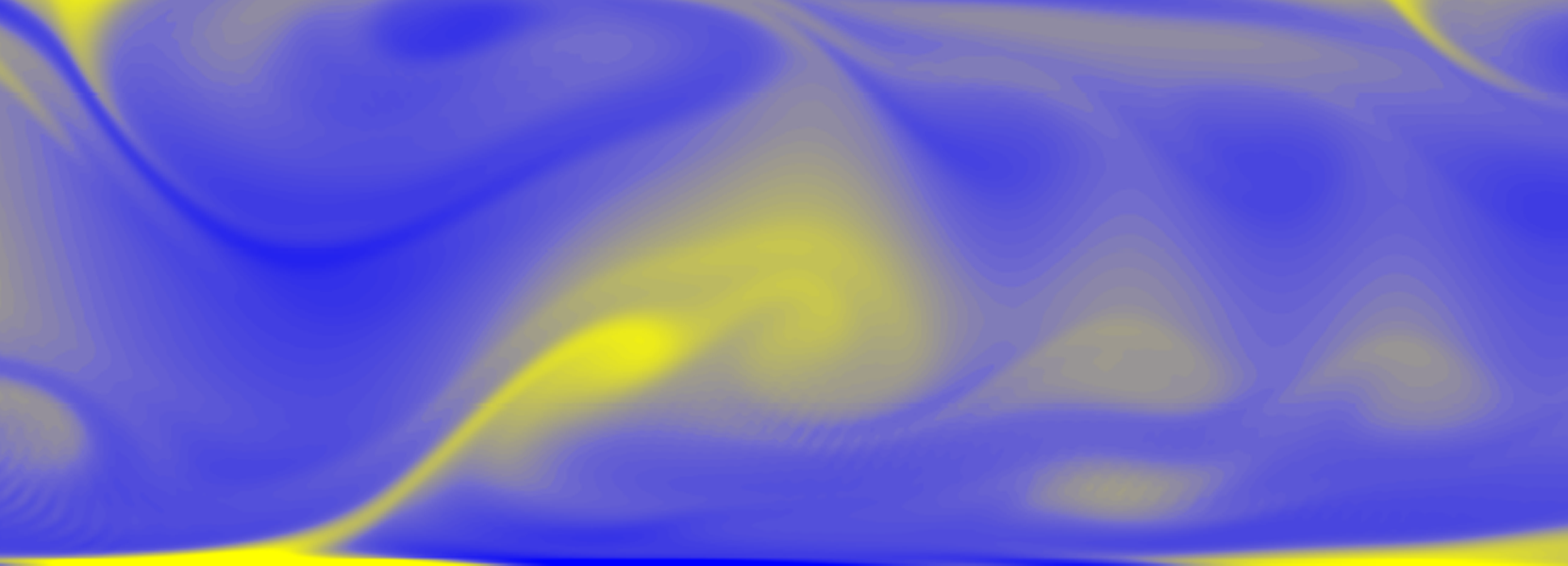
Multiphase turbulence is a complex phenomenon characterised by a wide range of scales in space and time. On the one hand, there are the scales of the flow-field, $\mathbf{u}$, which range from the largest ones -- of size comparable to the domain size -- down to the smallest ones, of size of the order of the Kolmogorov scale (the scale at which energy is dissipated by viscosity). On the other hand, there are the scales of the interface separating the two phases, whose size is comparable to that of the molecular scale. For this reason, performing an accurate simulation of a turbulent multiphase flow is at present extremely challenging. To tackle this problem, we propose here the adoption of a dual-grid approach, based on a combined pseudo-spectral DNS of turbulence, coupled with a Phase Field Method. We remark here that the Phase Field Method (PFM) is based on the introduction of an order parameter $\phi$ that is uniform in the bulk phases ($\phi=1$ in one phase, and $\phi=-1$ in the other phase), while it varies continuously over the interface separating the two phases. Since the solution of the Navier-Stokes equation to obtain the flow-field, $\mathbf{u}$, is extremely computationally demanding, we use two different computational grids: a reference grid for the flow field and pressure $\mathbf{u},\:p$ (i.e., fine enough to solve the flow down to the Kolmogorov scale), and a refined grid for the phase-field, $\phi$. The finer the resolution of the phase-field, $\phi$, the better the description of the interface deformation and of the morphology of the phase interaction. This is well represented in figure (\ref{fig:E}), where two simulations, with two different resolutions for the phase-field, $\phi$, are compared (in panel b, the resolution is twice compared to panel a). The performance of the current approach (in terms of reduction of computational time and required memory) has been evaluated for the well-known benchmark case of the deformation of a single drop in a two-dimensional flow. The applicability of the current method to a realistic 3D case has also been tested, by evaluating the dynamics of a thin sheet layer placed at the centre of a turbulent channel flow. The influence of the resolution of the phase-field, $\phi$ -- while keeping constant the resolution of the flow field, $\mathbf{u}$ -- on the dynamics of the flow and on the phase morphology (including also the droplet-size distribution) will be presented and discussed.